In the last lecture we learned how to make a compartmental model of a neuron, including models of voltage activated channels. This time, we will talk about what goes on in the dendrites and how this relates to the behavior of more complex cells and networks. The first step is to model synaptically (chemically) activated channels.
The variable conductance in the generic compartment diagram could also represent a synaptically activated channel, usually ocurring in a dendritic compartment.

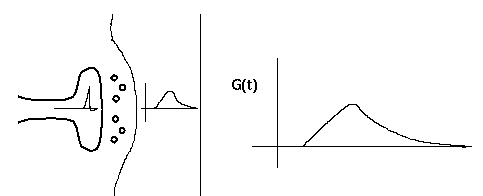
This diagram shows a synapse with an action potential propagating to the pre-synaptic terminal, causing neurotransmitter release, and the resulting post-synaptic conductance change, G(t).
There is a lot of biochemistry and molecular biology involved in this behavior. Fortunately, we can often use an empirical fit to the observed behavior, rather than modeling it in detail.
Typically, the conductance change from a quantum of neurotransmitter follows a linear rise and exponential decay, so it is often modeled with a so-called "alpha" function with a single time constant, tau.
G(t) = const * t * exp(-t/tau)
The current due to this conductance is
I = G(Ek - Vm),
which may be into or out of the cell, depending on the size of the ionic equilbrium potential Ek, relative to the membrane potential. Here we have adopted the convention that a positive current flows into the cell. Thus, if the Ek is large (Na or Ca), the current will be into the cell, and it will be a depolarizing (excitatory) synapse. If it is large and negative (Ek < Vm, as for potassium), it will be an inhibitory synapse. So, we can use the same model for both types of synapses.
These simulations will also let you experiment with "silent inhibition", in which a shunting, but slightly depolorizing PSP can have an inhibitory effect.
Other models use a difference of two exponentials, with two time constants. We'll use the alpha function model to understand both temporal and spatial summation of synaptic inputs.
Another time constant which is relevant for determining the properties of the cell is the membrane time constant, Rm * Cm. This represents the time that it takes to charge up the membrane capacitance, and will also affect the generation of a post-synaptic potential. Although we won't do it here, this simulation will let you see what happens if you have a small time constant for synaptic activation and a large membrane time constant.
This simulation has a help menu that can show a schematic diagram of the model neuron and the types of inputs that we can give to it.
We have a simple model neuron with a soma and two dendrite compartments which are connected by axial resistances, as well as the option of putting any number of passive cable compartments between these two dendrite compartments. These passive compartments are like the ones shown, but have no variable conductances. This will let us see what happens if we have spatially separated inputs to the neuron. The soma has Hodgkin-Huxley voltage activated channels like the ones we used in the last simulation, and the dendrite compartments have both excitatory and inhibitory synaptically activated channels which respond to spikes applied at the synapses. Not only can we change the various parameters of the cell by popping up menus, but we can apply different types of stimulation. For example, we can inject pulses of current into any of the compartments, or connect spike trains to any of the synapses with a specified weighting. We'll start by applying a burst of spikes 10 milliseconds apart to the Excitatory synapse in the first dendrite section.
The spike train starts after 10 milliseconds. {UPPER plot}
We can see that each spike causes a rise and decay in the conductance of this channel. {MIDDLE plot}
However, the conductance decays before the postsynaptic potential can build up to a very high level. {LOWER plot}
So, let's see what happens if we make the input spikes come four times as fast.
This is done in overlay mode, with the new results plotted in blue, so we can compare them with the previous results. (However, the plots of activation parameters and soma conductances were not overlayed, in order to keep the plots simple.)
Now, we are getting a good buildup up of conductance as each increase adds to the previous one, and we see action potentials both in the dendrite compartment {LOWER LEFT} and in the soma {LOWER RIGHT}. You might notice that the action potentials are a little higher in the soma. This is because the PSP in the dendrite is propagated to the soma, where the voltage activated channels cause the action potentials, and these are propagated back to the dendrite through an axial resistance. In the dendrite compartment, we're seeing a superposition of the PSP produced here and the action potential which is produced in the soma. If we were to look in a more distant dendrite section, the peaks would be much more attenuated. We'll do this in the next simulation run.
Now we'll explore the effects of summing spatially separated inputs to the neuron. Although it isn't shown on this diagram, I've added 5 passive cable sections between the two dendrite compartments, so dendrite compartment #2 is much further from the soma. With the dimensions and resistances which are used here, cable theory predicts that a voltage in this compartment will be attenuatated by about 50% by the time it gets to the soma. (This distance is 0.7 of the "space constant", so the attenuation is exp(-0.7).
You may want to consult the neuron inputs diagram to remind yourself of the location of the three compartments.
I've set the interval for both sources of spike trains to 2 msecs, but I'll start applying Source A to the excitatory input of dendrite #2 right away, and wait 60 msec before applying Source B to the inhibitory input of dendrite #1.
Since the excitatory input is further away, we'll give it a fighting chance by giving it a higher synaptic weight. The weight of 40 means that we are scaling the conductance as if 40 synapses were being made at this point in the dendrite. The inhibitory inputs to dendrite #1 gets half this weight. We do this because the input from a single synapse is rarely enough to fire an action potential, unless it is a motor neuron.
The excitatory spike train (in red) starts right away (Inputs to cell - UPPER LEFT), and causes a large buildup of conductance in the excitatory channel of the distal dendrite compartment {UPPER RIGHT}. This leads to a large increase in the membrane potential in this compartment - way above threshold.
This passively propagates to the soma where it produces action potentials. These are shown in slightly attenuated form in the nearby dendrite #1 compartment (LOWER LEFT), and in much more attenuated form in the distant dendrite #2 compartment (LOWER RIGHT). In this compartment, we can see the postsynaptic potential clearly, with the attenuated somatic action potentials superimposed.
After about 60 msec, the action potentials are disappearing. Let's look at our inputs and see what's happening. Now we are getting spikes to the inhibitory channel dendrite #1 {UPPER LEFT}. It produces a fairly small buildup of conductance {MIDDLE LEFT}, which produces a modest hyperpolaring influence in the compartment {LOWER LEFT}. But, since this compartment is close to the soma, it has a stronger effect than the depolarizing PSP in the distal dendrite compartment, and it stops the production of action potentials in the soma.
If we like, we can change the display to plot the soma membrane potential and see this directly.
We've seen two properties of neurons which are relevant to understanding the ways which neurons compute:
In the next lecture, we will look at the behavior of more complex neurons, and conclude with a model of a cortical network.
 Back
to Lectures on Computational Neuroscience
Back
to Lectures on Computational Neuroscience